qmt_bssfp : qMT using Balanced Steady State Free Precession acquisition¶
Contents
- 1. Print qmt_bssfp information
- 2. Setting model parameters
- 2.a. Create qmt_bssfp object
- 2.b. Set protocol and options
- 2.b.1 Set protocol the CLI way
- 2.b.2 Set protocol and options the GUI way
- 3. Fit MRI data
- 3.a. Load input data
- 3.b. Execute fitting process
- 3.c. Display FitResults
- 3.d. Save fit results
- 3.e. Re-use or share fit configuration files
- 4. Simulations
- 4.a. Single Voxel Curve
- 4.b. Sensitivity Analysis
- 5. Notes
- 5.a. Notes specific to qmt_bssfp
- 5.b. Generic notes
- 5.b.1. Batch friendly option and protocol conventions
- 5.b.2 Parallelization
- 6. Citations
% This m-file has been automatically generated using qMRgenBatch(qmt_bssfp) % for publishing documentation. % Command Line Interface (CLI) is well-suited for automatization % purposes and Octave. % % Please execute this m-file section by section to get familiar with batch % processing for qmt_bssfp on CLI. % % Demo files are downloaded into qmt_bssfp_data folder. % % Written by: Agah Karakuzu, 2017 % ==============================================================================
1. Print qmt_bssfp information
qMRinfo('qmt_bssfp');
qmt_bssfp : qMT using Balanced Steady State Free Precession acquisition ----------------------------------------------------------------------------------------------------- Assumptions: Inputs: MTdata 4D Magnetization Transfer data (R1map) 1/T1map (OPTIONAL) (Mask) Binary mask to accelerate the fitting (OPTIONAL) Outputs: F Ratio of number of restricted pool to free pool, defined as F = M0r/M0f = kf/kr. kr Exchange rate from the free to the restricted pool (note that kf and kr are related to one another via the definition of F. Changing the value of kf will change kr accordingly, and vice versa). R1f Longitudinal relaxation rate of the free pool (R1f = 1/T1f). R1r Longitudinal relaxation rate of the restricted pool (R1r = 1/T1r). T2f Tranverse relaxation time of the free pool (T2f = 1/R2f). M0f Equilibrium value of the free pool longitudinal magnetization. Additional Outputs M0r Equilibrium value of the restricted pool longitudinal magnetization. kf Exchange rate from the restricted to the free pool. resnorm Fitting residual. Protocol: MTdata Array [nbVols x 2]: Alpha Flip angle of the RF pulses (degrees) Trf Duration of the RF pulses (s) Options: RF Pulse Shape Shape of the RF pulses. Available shapes are: - hard - gaussian - gausshann (gaussian pulse with Hanning window) - sinc - sinchann (sinc pulse with Hanning window) - singauss (sinc pulse with gaussian window) - fermi Nb of RF pulses Number of RF pulses applied before readout. Protocol Timing Fix TR Select this option and enter a value in the text box below to set a fixed repetition time. Fix TR - Trf Select this option and enter a value in the text box below to set a fixed free precession time (TR - Trf). Prepulse Perform an Alpha/2 - TR/2 prepulse before each series of RF pulses. R1 Use R1map to By checking this box, you tell the fitting constrain R1f algorithm to check for an observed R1map and use its value to constrain R1f. Checking this box will automatically set the R1f fix box to true in the Fit parameters table. Fix R1r = R1f By checking this box, you tell the fitting algorithm to fix R1r equal to R1f. Checking this box will automatically set the R1r fix box to true in the Fit parameters table. Global G(0) The assumed value of the absorption lineshape of the restricted pool. References: Please cite the following if you use this module: In addition to citing the package: Karakuzu A., Boudreau M., Duval T.,Boshkovski T., Leppert I.R., Cabana J.F., Gagnon I., Beliveau P., Pike G.B., Cohen-Adad J., Stikov N. (2020), qMRLab: Quantitative MRI analysis, under one umbrella doi: 10.21105/joss.02343 Reference page in Doc Center doc qmt_bssfp
2. Setting model parameters
2.a. Create qmt_bssfp object
Model = qmt_bssfp;
2.b. Set protocol and options
Protocol: MRI acquisition parameters that are accounted for by the respective model.
For example: TE, TR, FA FieldStrength. The assigned protocol values are subjected to a sanity check to ensure that they are in agreement with the data attributes.
Options: Fitting preferences that are left at user's discretion.
For example: linear fit, exponential fit, drop first echo.
2.b.1 Set protocol the CLI way
If you are using Octave, or would like to serialize your operations any without GUI involvement, you can assign protocol directly in CLI:
Alpha = [5.0000; 10.0000; 15.0000; 20.0000; 25.0000; 30.0000; 35.0000; 40.0000; 35.0000; 35.0000; 35.0000; 35.0000; 35.0000; 35.0000; 35.0000; 35.0000]; % Alpha is a vector of [16X1] Trf = [0.0003; 0.0003; 0.0003; 0.0003; 0.0003; 0.0003; 0.0003; 0.0003; 0.0002; 0.0003; 0.0004; 0.0006; 0.0008; 0.0012; 0.0016; 0.0021]; % Trf is a vector of [16X1] Model.Prot.MTdata.Mat = [ Alpha Trf];
See the generic notes section below for further information.
2.b.2 Set protocol and options the GUI way
The following command opens a panel to set protocol and options (if GUI is available to the user):
Model = Custom_OptionsGUI(Model);
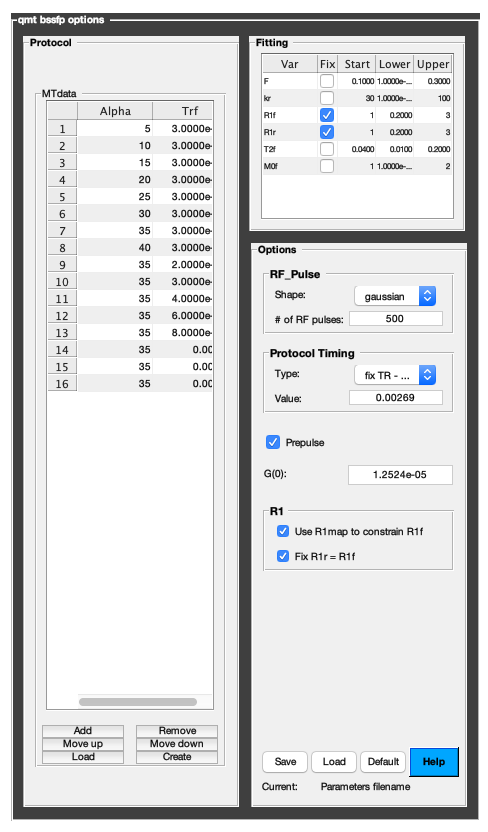
If available, you need to close this panel for the remaining of the script to proceed.
Using this panel, you can save qMRLab protocol files that can be used in both interfaces. See the generic notes section below for details.
3. Fit MRI data
3.a. Load input data
This section shows how you can load data into a(n) qmt_bssfp object.
- At the CLI level, qMRLab accepts structs containing (double) data in the fields named in accordance with a qMRLab model.
See the generic notes section below for BIDS compatible wrappers and scalable
qMRLab workflows.
% |- qmt_bssfp object needs 3 data input(s) to be assigned: % |- MTdata % |- R1map % |- Mask data = struct(); % MTdata.nii.gz contains [128 128 1 16] data. data.MTdata=double(load_nii_data('qmt_bssfp_data/MTdata.nii.gz')); % R1map.nii.gz contains [128 128] data. data.R1map=double(load_nii_data('qmt_bssfp_data/R1map.nii.gz')); % Mask.nii.gz contains [128 128] data. data.Mask=double(load_nii_data('qmt_bssfp_data/Mask.nii.gz'));
3.b. Execute fitting process
This section will fit the loaded data.
FitResults = FitData(data,Model,0);
Visit the generic notes section below for instructions to accelerate fitting by
parallelization using ParFitData.
3.c. Display FitResults
You can display the current outputs by:
qMRshowOutput(FitResults,data,Model);
A representative fit curve will be plotted if available.
To render images in this page, we will load the fit results that had been saved before. You can skip the following code block;
% Load FitResults that comes with the example dataset. FitResults_old = load('FitResults/FitResults.mat'); qMRshowOutput(FitResults_old,data,Model);
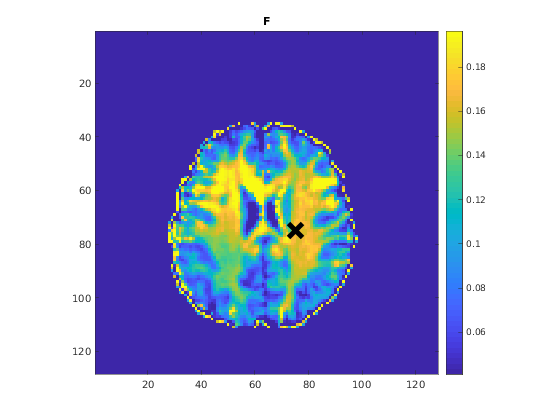
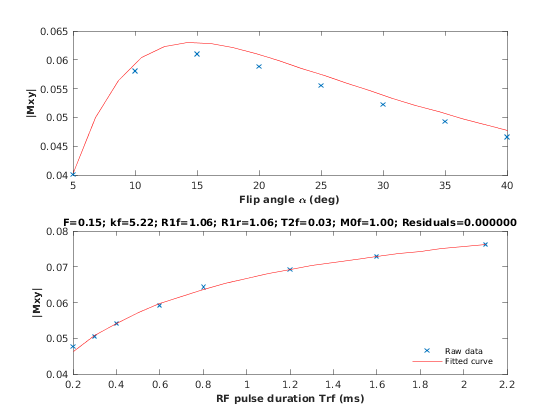
3.d. Save fit results
Outputs can be saved as *.nii.(gz) if NIfTI inputs are available:
% Generic function call to save nifti outputs FitResultsSave_nii(FitResults, 'reference/nifti/file.nii.(gz)');
If not, FitResults.mat file can be saved. This file contains all the outputs as workspace variables:
% Generic function call to save FitResults.mat
FitResultsSave_mat(FitResults);
FitResults.mat files can be loaded to qMRLab GUI for visualization and ROI
analyses.
The section below will be dynamically generated in accordance with the example data format (mat or nii). You can substitute FitResults_old with FitResults if you executed the fitting using example dataset for this model in section 3.b..
FitResultsSave_nii(FitResults_old, 'qmt_bssfp_data/MTdata.nii.gz');
3.e. Re-use or share fit configuration files
qMRLab's fit configuration files (qmt_bssfp_Demo.qmrlab.mat) store all the options and protocol in relation to the used model and the release version.
*.qmrlab.mat files can be easily shared with collaborators to allow them fit their own
data or run simulations using identical option and protocol configurations.
Model.saveObj('my_qmt_bssfp_config.qmrlab.mat');
4. Simulations
4.a. Single Voxel Curve
Simulates single voxel curves
x = struct; x.F = 0.1; x.kr = 30; x.R1f = 1; x.R1r = 1; x.T2f = 0.04; x.M0f = 1; % Set simulation options Opt.SNR = 50; Opt.Method = 'Analytical equation'; Opt.ResetMz = false; % run simulation figure('Name','Single Voxel Curve Simulation'); FitResult = Model.Sim_Single_Voxel_Curve(x,Opt);
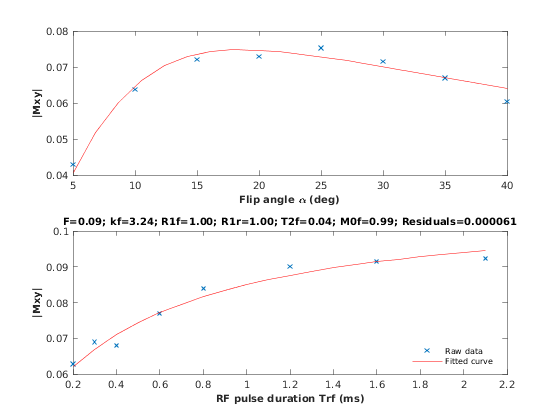
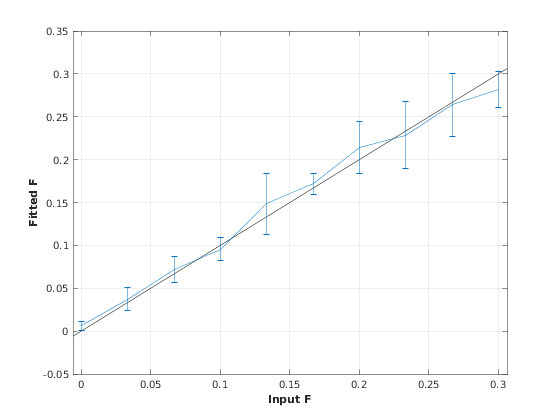
4.b. Sensitivity Analysis
Simulates sensitivity to fitted parameters
F kr R1f R1r T2f M0f
OptTable.st = [0.1 30 1 1 0.04 1]; % nominal values OptTable.fx = [0 1 1 1 1 1]; %vary F... OptTable.lb = [0.0001 0.0001 0.2 0.2 0.01 0.0001]; %...from 0.0001 OptTable.ub = [0.3 1e+02 3 3 0.2 2]; %...to 0.3 % Set simulation options Opt.SNR = 50; Opt.Method = 'Analytical equation'; Opt.ResetMz = false; Opt.Nofrun = 5; % run simulation SimResults = Model.Sim_Sensitivity_Analysis(OptTable,Opt); figure('Name','Sensitivity Analysis'); SimVaryPlot(SimResults, 'F' ,'F' );
5. Notes
5.a. Notes specific to qmt_bssfp
Not provided.
5.b. Generic notes
5.b.1. Batch friendly option and protocol conventions
If you would like to load a desired set of options / protocols programatically, you can use *.qmrlab.mat files. To save a configuration from the protocol panel of qmt_bssfp, first open the respective panel by running the following command in your MATLAB command window (MATLAB only):
Custom_OptionsGUI(qmt_bssfp);
In this panel, you can arrange available options and protocols according to your needs, then click the save button to save my_qmt_bssfp.qmrlab.mat file. This file can be later loaded into a qmt_bssfp object in batch by:
Model = qmt_bssfp;
Model = Model.loadObj('my_qmt_bssfp.qmrlab.mat');
Model.loadObj('my_qmt_bssfp.qmrlab.mat') call won't update the fields in the Model object, unless the output is assigned to the object as shown above. This compromise on convenience is to retain Octave CLI compatibility.
If you don't have MATLAB, hence cannot access the GUI, two alternatives are available to populate options:
- Use qmrlab/mcrgui:latest Docker image to access GUI. The instructions are available here.
- Set options and protocols in CLI:
- List available option fields using tab completion in Octave's command prompt (or window)
Model = qmt_bssfp;
Model.option. % click the tab button on your keyboard and list the available fields.
- Assign the desired field. For example, for a mono_t2 object:
Model = mono_t2; Model.options.DropFirstEcho = true; Model.options.OffsetTerm = false;
Some option fields may be mutually exclusive or interdependent. Such cases are handled by the GUI options panel; however, not exposed to the CLI. Therefore, manual CLI options assignments may be challenging for some involved methods such as qmt_spgr or qsm_sb. If above options are not working for you and you cannot infer how to set options solely in batch, please feel free to open an issue in qMRLab and request the protocol file you need.
Similarly, in CLI, you can inspect and assign the protocols:
Model = qmt_bssfp;
Model.Prot. % click the tab button on your keyboard and list the available fields.
Each protocol field has two subfields of Format and Mat. The first one is a cell indicating the name of the protocol parameter (such as EchoTime (ms)) and the latter one contains the respective values (such as 30 x 1 double array containing EchoTimes).
The default Mat protocol values are set according to the example datasets served via OSF.
5.b.2 Parallelization
Beginning from release 2.5.0, you can accelerate fitting for the voxelwise models using parallelization.
Available in MATLAB only. Requires parallel processing toolbox.
In CLI, you can perform parallel fitting by:
parpool(); FitResults = ParFitData(data,Model);
If a parpool exists, the ParFitData will use it. If not, a new pool will be created using the local profile. By default, ParFitData saves outputs automatically every 5 minutes. You can disable this feature by:
FitResults = ParFitData(data, Model, 'AutosaveEnabled', false);
Alternatively, you can change the autosave interval (min 1 min) by:
FitResults = ParFitData(data,Model,'AutoSaveInterval',10);
If something went wrong during the fitting (e.g. your computer had to be restarted), you can recover the autosaved data by:
FitResults = ParFitData(data,Model,'RecoverDirectory','/ParFitTempResults_*/folder/from/the/previous/session');
GUI users will be prompted a question about whether they would like to use parallelization after clicking the Fit Data button, if the conditions are met. When called from GUI, ParFitData will be run with default options:
- Save temporary results every 5 minutes or whenever a chunk has finished processing
- Split data into chunks with a granularity factor of 3
- Do not remove temporary fit results upon completion
For further information:
help ParFitData
The default parallelization options can be changed in the preferences.json file located at the root qMRLab directory.
6. Citations
qMRLab JOSS article
Karakuzu A., Boudreau M., Duval T.,Boshkovski T., Leppert I.R., Cabana J.F., Gagnon I., Beliveau P., Pike G.B., Cohen-Adad J., Stikov N. (2020), qMRLab: Quantitative MRI analysis, under one umbrella 10.21105/joss.02343
Reference article for qmt_bssfp
Quantitative MRI, under one umbrella.
NeuroPoly Lab, Montreal, Canada