dti: Compute a tensor from diffusion data¶
Contents
- 1. Print dti information
- 2. Setting model parameters
- 2.a. Create dti object
- 2.b. Set protocol and options
- 2.b.1 Set protocol the CLI way
- 2.b.2 Set protocol and options the GUI way
- 3. Fit MRI data
- 3.a. Load input data
- 3.b. Execute fitting process
- 3.c. Display FitResults
- 3.d. Save fit results
- 3.e. Re-use or share fit configuration files
- 4. Simulations
- 4.a. Single Voxel Curve
- 4.b. Sensitivity Analysis
- 5. Notes
- 5.a. Notes specific to dti
- 5.b. Generic notes
- 5.b.1. Batch friendly option and protocol conventions
- 5.b.2 Parallelization
- 6. Citations
% This m-file has been automatically generated using qMRgenBatch(dti) % for publishing documentation. % Command Line Interface (CLI) is well-suited for automatization % purposes and Octave. % % Please execute this m-file section by section to get familiar with batch % processing for dti on CLI. % % Demo files are downloaded into dti_data folder. % % Written by: Agah Karakuzu, 2017 % ==============================================================================
1. Print dti information
qMRinfo('dti');
dti: Compute a tensor from diffusion data Assumptions: Anisotropic Gaussian diffusion tensor Valid at relatively low b-value (i.e. ~< 2000 s/mm2) Inputs: DiffusionData 4D DWI (SigmaNoise) map of the standard deviation of the noise per voxel. (OPTIONAL) (Mask) Binary mask to accelerate the fitting. (OPTIONAL) Outputs: D [Dxx Dxy Dxz Dxy Dyy Dyz Dxz Dyz Dzz] Diffusion Tensor L1 1rst eigenvalue of D L2 2nd eigenvalue of D L3 3rd eigenvalue of D FA Fractional Anisotropy: FA = sqrt(3/2)*sqrt(sum((L-L_mean).^2))/sqrt(sum(L.^2)); S0_TEXX Signal at b=0 at TE=XX (residue) Fitting residuals Protocol: At least 2 shells (e.g. b=1000 and b=0 s/mm2) diffusion gradient direction in 3D DiffusionData Array [NbVol x 7] Gx Diffusion Gradient x Gy Diffusion Gradient y Gz Diffusion Gradient z Gnorm (T/m) Diffusion gradient magnitude Delta (s) Diffusion separation delta (s) Diffusion duration TE (s) Echo time Options: fitting type 'linear' Solves the linear problem (ln(S/S0) = -bD) 'non-linear (Rician Likelihood)' Add an additional fitting step, using the Rician Likelihood. Rician noise bias only for non-linear fitting SigmaNoise map is prioritary. 'Compute Sigma per voxel' Sigma is estimated by computing the STD across repeated scans. 'fix sigma' Use scd_noise_std_estimation to measure noise level. Use 'value' to fix Sigma. Example of command line usage (see dti_batch.html): Model = dti %% LOAD DATA data.DiffusionData = load_nii_data('DiffusionData.nii.gz'); data.SigmaNoise = load_nii_data('SigmaNoise.nii.gz'); data.Mask = load_nii_data('Mask.nii.gz'); %% FIT A SINGLE VOXEL % Specific voxel: datavox = extractvoxel(data,voxel); % Interactive selection: datavox = extractvoxel(data); voxel = round(size(data.DiffusionData(:,:,:,1))/2); % pick FOV center datavox = extractvoxel(data,voxel); FitResults = Model.fit(datavox); Model.plotModel(FitResults, datavox); % plot fit results %% FIT all voxels FitResults = FitData(data,Model); % SAVE results to NIFTI FitResultsSave_nii(FitResults,'DiffusionData.nii.gz'); % use header from 'DiffusionData.nii.gz' For more examples: qMRusage(dti) Author: Tanguy Duval, 2016 References: Please cite the following if you use this module: Basser, P.J., Mattiello, J., LeBihan, D., 1994. MR diffusion tensor spectroscopy and imaging. Biophys. J. 66, 259?267. In addition to citing the package: Karakuzu A., Boudreau M., Duval T.,Boshkovski T., Leppert I.R., Cabana J.F., Gagnon I., Beliveau P., Pike G.B., Cohen-Adad J., Stikov N. (2020), qMRLab: Quantitative MRI analysis, under one umbrella doi: 10.21105/joss.02343 Reference page in Doc Center doc dti
2. Setting model parameters
2.a. Create dti object
Model = dti;
2.b. Set protocol and options
Protocol: MRI acquisition parameters that are accounted for by the respective model.
For example: TE, TR, FA FieldStrength. The assigned protocol values are subjected to a sanity check to ensure that they are in agreement with the data attributes.
Options: Fitting preferences that are left at user's discretion.
For example: linear fit, exponential fit, drop first echo.
2.b.1 Set protocol the CLI way
If you are using Octave, or would like to serialize your operations any without GUI involvement, you can assign protocol directly in CLI:
Gx = [0.0000; 0.0000; 0.6528; -0.3734; 0.6595; 0.4251; 0.9307; 0.2346; -0.5629; -0.1656; -0.9726; -0.0150; 0.1463; -0.2313; 0.7377; -0.7661; -0.1051; 0.0000; 0.3909; 0.1496; -0.9334; 0.1903; -0.7039; -0.5217; 0.9662; -0.3714; -0.7828; 0.8305; -0.3302; -0.2348; 0.0253; -0.5469; 0.7053; 0.0000; 0.3198; 0.7962; 0.8699; 0.6890; -0.9299; 0.0387; 0.3218; 0.3582; 0.8944; 0.4384; -0.3516; -0.1507; -0.5361; 0.5114; -0.0808; 0.0000; -0.0261; -0.4804; -0.8220; -0.3674; -0.8059; 0.9937; -0.9844; -0.4309; 0.1316; -0.0096; 0.6996; -0.6609; 0.8179; -0.7977; 0.4352; 0.0000; 0.3330; 0.5147; -0.8173; -0.5177; -0.0540; 0.0108; -0.0691; 0.8929; 0.6656; 0.3998; 0.2992; -0.6774; -0.3221; 0.5112; -0.1681; 0.0000; 0.8415; 0.2496; 0.6320; 0.1861; 0.4758; 0.7481; 0.9338; 0.6610; 0.6125; 0.6137; 0.6817; 0.0996; -0.9739; 0.8386; 0.2920; 0.0000; -0.7056; -0.2181; -0.6203; 0.0020; -0.1074; 0.2822; 0.4012; 0.5307; 0.5323; 0.9651; 0.0000]; % Gx is a vector of [109X1] Gy = [0.0000; 0.0000; -0.6550; 0.1688; 0.7394; 0.0347; 0.0616; -0.8169; -0.0797; -0.8647; 0.0079; 0.9886; 0.7658; -0.5711; 0.5254; 0.5946; -0.9930; 0.0000; -0.4079; -0.3372; -0.2009; 0.7622; -0.4547; 0.4241; -0.2577; 0.9198; 0.6149; -0.2333; -0.8437; -0.5578; 0.1522; -0.7771; 0.6419; 0.0000; -0.6674; -0.0672; -0.1770; 0.4593; 0.3590; 0.4492; 0.4365; 0.2082; 0.4341; -0.8638; 0.8508; 0.5115; 0.3158; -0.7514; 0.9207; 0.0000; -0.9526; -0.8692; 0.3566; -0.3033; -0.5619; -0.0273; -0.1502; -0.9023; 0.1687; -0.1114; -0.7110; -0.2140; -0.3778; -0.1210; 0.6742; 0.0000; -0.5741; -0.6575; -0.5127; 0.4818; 0.5946; -0.8315; -0.7675; 0.2597; 0.3549; -0.8171; -0.0563; -0.1344; 0.2540; 0.6731; -0.9515; 0.0000; -0.4352; 0.9109; -0.0796; -0.9773; -0.8795; 0.6348; -0.2954; -0.0966; -0.4925; -0.1628; -0.4899; 0.3862; -0.2261; 0.5426; 0.9388; 0.0000; 0.1116; 0.9406; 0.7701; 0.3742; -0.4286; -0.6551; 0.7562; 0.4305; 0.4358; -0.2538; 0.0000]; % Gy is a vector of [109X1] Gz = [0.0000; 0.0000; 0.3807; 0.9122; 0.1356; -0.9045; 0.3607; -0.5270; -0.8227; 0.4743; 0.2325; -0.1496; -0.6262; -0.7876; -0.4240; 0.2441; 0.0536; 0.0000; 0.8251; 0.9295; -0.2972; 0.6187; 0.5456; 0.7403; -0.0065; -0.1266; 0.0958; 0.5057; -0.4233; 0.7961; 0.9880; 0.3116; 0.3009; 0.0000; 0.6726; -0.6012; -0.4604; 0.5607; -0.0796; 0.8926; -0.8402; 0.9101; -0.1075; -0.2483; 0.3905; 0.8460; -0.7829; 0.4170; -0.3819; 0.0000; -0.3031; 0.1170; 0.4439; -0.8792; -0.1865; 0.1090; 0.0921; 0.0165; -0.9768; 0.9937; 0.0714; 0.7193; 0.4339; -0.5907; -0.5967; 0.0000; -0.7480; -0.5502; -0.2629; -0.7070; -0.8022; 0.5555; -0.6373; -0.3679; 0.6565; 0.4153; 0.9525; 0.7233; 0.9120; 0.5345; -0.2576; 0.0000; 0.3202; -0.3285; -0.7708; -0.1011; 0.0065; -0.1930; -0.2018; 0.7442; 0.6183; -0.7725; -0.5434; 0.9170; -0.0219; -0.0485; 0.1827; 0.0000; -0.6998; 0.2600; 0.1488; 0.9274; 0.8971; -0.7009; -0.5169; 0.7301; -0.7258; 0.0647; 0.0000]; % Gz is a vector of [109X1] Gnorm = [0.0000; 0.0000; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0310; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0000; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0310; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0000; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0310; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0000; 0.0800; 0.0566; 0.0800; 0.0800; 0.0310; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0000; 0.0566; 0.0800; 0.0800; 0.0310; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0000; 0.0800; 0.0800; 0.0310; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0000; 0.0800; 0.0310; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0800; 0.0800; 0.0566; 0.0000]; % Gnorm is a vector of [109X1] Delta = [0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308; 0.0308]; % Delta is a vector of [109X1] delta = [0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128; 0.0128]; % delta is a vector of [109X1] TE = [0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636; 0.0636]; % TE is a vector of [109X1] Model.Prot.DiffusionData.Mat = [ Gx Gy Gz Gnorm Delta delta TE];
See the generic notes section below for further information.
2.b.2 Set protocol and options the GUI way
The following command opens a panel to set protocol and options (if GUI is available to the user):
Model = Custom_OptionsGUI(Model);

If available, you need to close this panel for the remaining of the script to proceed.
Using this panel, you can save qMRLab protocol files that can be used in both interfaces. See the generic notes section below for details.
3. Fit MRI data
3.a. Load input data
This section shows how you can load data into a(n) dti object.
- At the CLI level, qMRLab accepts structs containing (double) data in the fields named in accordance with a qMRLab model.
See the generic notes section below for BIDS compatible wrappers and scalable
qMRLab workflows.
% |- dti object needs 3 data input(s) to be assigned: % |- DiffusionData % |- SigmaNoise % |- Mask data = struct(); % DiffusionData.nii.gz contains [74 87 50 109] data. data.DiffusionData=double(load_nii_data('dti_data/DiffusionData.nii.gz')); % Mask.nii.gz contains [74 87 50] data. data.Mask=double(load_nii_data('dti_data/Mask.nii.gz'));
3.b. Execute fitting process
This section will fit the loaded data.
FitResults = FitData(data,Model,0);
Visit the generic notes section below for instructions to accelerate fitting by
parallelization using ParFitData.
3.c. Display FitResults
You can display the current outputs by:
qMRshowOutput(FitResults,data,Model);
A representative fit curve will be plotted if available.
To render images in this page, we will load the fit results that had been saved before. You can skip the following code block;
% Load FitResults that comes with the example dataset. FitResults_old = load('FitResults/FitResults.mat'); qMRshowOutput(FitResults_old,data,Model);
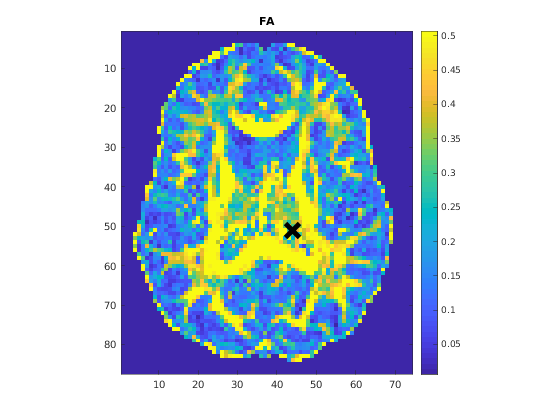
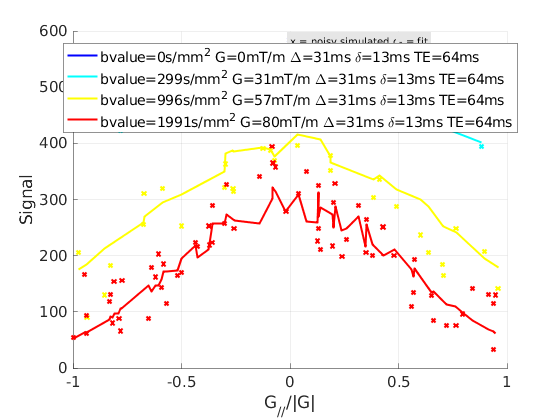
3.d. Save fit results
Outputs can be saved as *.nii.(gz) if NIfTI inputs are available:
% Generic function call to save nifti outputs FitResultsSave_nii(FitResults, 'reference/nifti/file.nii.(gz)');
If not, FitResults.mat file can be saved. This file contains all the outputs as workspace variables:
% Generic function call to save FitResults.mat
FitResultsSave_mat(FitResults);
FitResults.mat files can be loaded to qMRLab GUI for visualization and ROI
analyses.
The section below will be dynamically generated in accordance with the example data format (mat or nii). You can substitute FitResults_old with FitResults if you executed the fitting using example dataset for this model in section 3.b..
FitResultsSave_nii(FitResults_old, 'dti_data/DiffusionData.nii.gz');
3.e. Re-use or share fit configuration files
qMRLab's fit configuration files (dti_Demo.qmrlab.mat) store all the options and protocol in relation to the used model and the release version.
*.qmrlab.mat files can be easily shared with collaborators to allow them fit their own
data or run simulations using identical option and protocol configurations.
Model.saveObj('my_dti_config.qmrlab.mat');
4. Simulations
4.a. Single Voxel Curve
Simulates single voxel curves
x = struct; x.L1 = 2; x.L2 = 0.7; x.L3 = 0.7; Opt.SNR = 50; % run simulation figure('Name','Single Voxel Curve Simulation'); FitResult = Model.Sim_Single_Voxel_Curve(x,Opt);
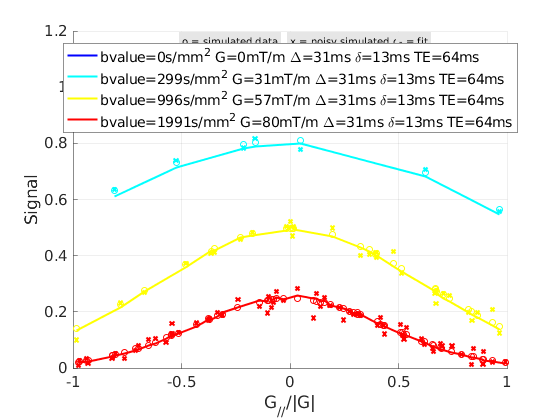
4.b. Sensitivity Analysis
Simulates sensitivity to fitted parameters
L1 L2 L3
OptTable.st = [2 0.7 0.7]; % nominal values OptTable.fx = [0 1 1]; %vary L1... OptTable.lb = [0 0 0]; %...from 0 OptTable.ub = [5 5 5]; %...to 5 Opt.SNR = 50; Opt.Nofrun = 5; % run simulation SimResults = Model.Sim_Sensitivity_Analysis(OptTable,Opt); figure('Name','Sensitivity Analysis'); SimVaryPlot(SimResults, 'L1' ,'L1' );
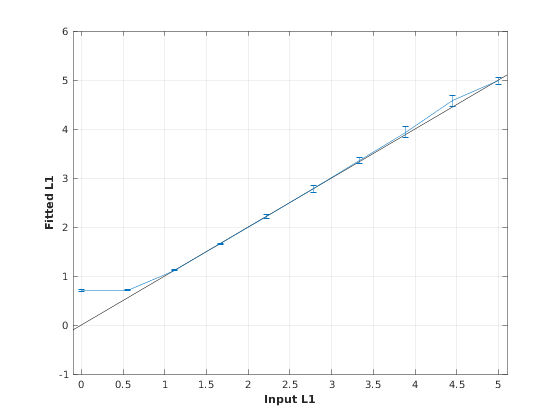
5. Notes
5.a. Notes specific to dti
Not provided.
5.b. Generic notes
5.b.1. Batch friendly option and protocol conventions
If you would like to load a desired set of options / protocols programatically, you can use *.qmrlab.mat files. To save a configuration from the protocol panel of dti, first open the respective panel by running the following command in your MATLAB command window (MATLAB only):
Custom_OptionsGUI(dti);
In this panel, you can arrange available options and protocols according to your needs, then click the save button to save my_dti.qmrlab.mat file. This file can be later loaded into a dti object in batch by:
Model = dti;
Model = Model.loadObj('my_dti.qmrlab.mat');
Model.loadObj('my_dti.qmrlab.mat') call won't update the fields in the Model object, unless the output is assigned to the object as shown above. This compromise on convenience is to retain Octave CLI compatibility.
If you don't have MATLAB, hence cannot access the GUI, two alternatives are available to populate options:
- Use qmrlab/mcrgui:latest Docker image to access GUI. The instructions are available here.
- Set options and protocols in CLI:
- List available option fields using tab completion in Octave's command prompt (or window)
Model = dti;
Model.option. % click the tab button on your keyboard and list the available fields.
- Assign the desired field. For example, for a mono_t2 object:
Model = mono_t2; Model.options.DropFirstEcho = true; Model.options.OffsetTerm = false;
Some option fields may be mutually exclusive or interdependent. Such cases are handled by the GUI options panel; however, not exposed to the CLI. Therefore, manual CLI options assignments may be challenging for some involved methods such as qmt_spgr or qsm_sb. If above options are not working for you and you cannot infer how to set options solely in batch, please feel free to open an issue in qMRLab and request the protocol file you need.
Similarly, in CLI, you can inspect and assign the protocols:
Model = dti;
Model.Prot. % click the tab button on your keyboard and list the available fields.
Each protocol field has two subfields of Format and Mat. The first one is a cell indicating the name of the protocol parameter (such as EchoTime (ms)) and the latter one contains the respective values (such as 30 x 1 double array containing EchoTimes).
The default Mat protocol values are set according to the example datasets served via OSF.
5.b.2 Parallelization
Beginning from release 2.5.0, you can accelerate fitting for the voxelwise models using parallelization.
Available in MATLAB only. Requires parallel processing toolbox.
In CLI, you can perform parallel fitting by:
parpool(); FitResults = ParFitData(data,Model);
If a parpool exists, the ParFitData will use it. If not, a new pool will be created using the local profile. By default, ParFitData saves outputs automatically every 5 minutes. You can disable this feature by:
FitResults = ParFitData(data, Model, 'AutosaveEnabled', false);
Alternatively, you can change the autosave interval (min 1 min) by:
FitResults = ParFitData(data,Model,'AutoSaveInterval',10);
If something went wrong during the fitting (e.g. your computer had to be restarted), you can recover the autosaved data by:
FitResults = ParFitData(data,Model,'RecoverDirectory','/ParFitTempResults_*/folder/from/the/previous/session');
GUI users will be prompted a question about whether they would like to use parallelization after clicking the Fit Data button, if the conditions are met. When called from GUI, ParFitData will be run with default options:
- Save temporary results every 5 minutes or whenever a chunk has finished processing
- Split data into chunks with a granularity factor of 3
- Do not remove temporary fit results upon completion
For further information:
help ParFitData
The default parallelization options can be changed in the preferences.json file located at the root qMRLab directory.
6. Citations
qMRLab JOSS article
Karakuzu A., Boudreau M., Duval T.,Boshkovski T., Leppert I.R., Cabana J.F., Gagnon I., Beliveau P., Pike G.B., Cohen-Adad J., Stikov N. (2020), qMRLab: Quantitative MRI analysis, under one umbrella 10.21105/joss.02343
Reference article for dti
Quantitative MRI, under one umbrella.
NeuroPoly Lab, Montreal, Canada